МЕТОДИКАИ ТАЪЛИМИ ОМӮЗИШИ МАФҲУМИ МОДЕЛИРОНӢ

Моделиронӣ — ин усули маърифати буда, аз бунёди модел ва таҳқиқи онҳо иборат аст. Ҳар як объект дорои миқдори хеле зиёди хосиятҳои гуногун мебошад. Ин объекти ба таври сунъӣ сохташуда, дар намуди схемаҳо, формулаҳои математикӣ, шаклҳои физикӣ, дастаи маълумотҳо ва алгоритми коркарди онҳо ва ғайра мебошад. Дар раванди сохтани модел хосиятҳои асосӣ, аз ҳама муҳим ҷудо карда мешаванд.
Мақсади таълими моделиронӣ
Омӯзиши моделиронӣ бояд донишҳои асосиро дар бораи назарияи моделсозӣ, масолеҳ, технологияҳои сохтмон ва барномаҳои компютерӣ фаро гирад. Инкишофи малакаҳои амалӣ: хонандагон бояд малакаҳои кории амалиро бо асбобҳо ва масолеҳ, инчунин, қобилияти истифодаи барномаҳои компютериро барои сохтани моделҳо омӯзанд. Омӯзиши моделиронӣ ба рушди тафаккури фазоӣ, тасаввуроти эҷодӣ, ҳалли мушкилот ва қобилияти кори дастаҷамъона мусоидат мекунад. Омӯзиши моделиронӣ метавонад заминаи хубе барои интихоби касб дар соҳаҳои муҳандисӣ, меъморӣ, тарроҳӣ ва ғайра, бошад.
Принсипҳои методикаи таълим
Омӯзиши моделиронӣ бояд фаъол бошад, ки дар он хонандагон на танҳо ба назария гӯш медиҳанд, балки дар раванди сохтани моделҳо фаъолона ширкат мекунанд. Омӯзиш бояд аз содатарин моделҳо оғоз шуда, тадриҷан ба моделҳои мураккаб гузарад. Ин ба хонандагон имкон медиҳад, ки тадриҷан дониш ва малакаҳои худро инкишоф диҳанд. Истифодаи моделҳои омода, расмҳо, видеоҳо ва дигар воситаҳои визуалӣ ба хонандагон имкон медиҳад, ки назарияро беҳтар дарк кунанд.
Истифодаи технологияҳои муосир
Барномаҳои компютерии моделсозӣ, принтерҳои 3D ва дигар технологияҳои муосир ба омӯзиш ҷолибияти бештар мебахшанд ва имкониятҳои навро фароҳам меоранд.
Супориши амалӣ
Супориши амалӣ ба хонандагон имкон медиҳад, ки дониши худро дар амал татбиқ намоянд, малакаҳои худро инкишоф диҳанд ва масъулияти худро барои натиҷаи кор эҳсос кунанд. Кор дар гурӯҳҳо ба хонандагон имкон медиҳад, ки малакаҳои ҳамкорӣ, муошират ва ҳалли мушкилотро инкишоф диҳанд.
Равиши дарс
Ҳар як хонанда дорои хусусиятҳои хоси худ аст. Омӯзгор бояд ба сатҳи дониш, манфиатҳо ва талаботи ҳар як хонанда таваҷҷуҳ зоҳир намояд ва усулҳои таълимро мувофиқи интизориҳо ва дониши онҳо мутобиқ созад.
Усулҳои таълим
Баёни мавзуъ: омӯзгори фаннӣ мавзуи навро баён мекунад ва ба хонандагон барои ба пурраагӣ мавзӯи навро қабул кардан мисолҳо меорад.
Намоиш: Омӯзгор раванди сохтани моделро нишон медиҳад.
Корҳои амалӣ: Хонандагон бо роҳбарии омӯзгор моделҳо месозанд.
Лоиҳаҳо: Хонандагон баъди супориши амалиро ба иҷро расонидан, бояд дар гурӯҳҳо лоиҳаҳои мураккабтарро таҳия ва амалӣ кунанд.
Саволҳо ва муҳокимаҳо: Омӯзгор ба хонандагон саволҳо медиҳад ва муҳокимаҳо мегузаронад, то дарки мавзуъро тафтиш намояд.
Натиҷагирӣ: яке аз равишҳои тарзи гузариши дарс бо методи салоҳиятнок ин натиҷагирӣ мебошад, ки барои кори омӯзгор хеле шарт, зарур ва муфид мебошад.
Омӯзиши моделиронӣ метавонад ба хонандагон имкониятҳои васеъро фароҳам оварад, аз ҷумла, ташаккули донишҳои асосӣ, инкишофи малакаҳои амалӣ, рушди тафаккури фазоӣ ва мантиқӣ, инчунин, омодагӣ ба фаъолияти касбӣ. Методикаи самараноки таълим бояд фаъол, ҷолиб, мутобиқшаванда ва ба талаботи хонандагон мувофиқ бошад. Бо истифодаи усулҳои гуногун ва воситаҳои таълими муосир, омӯзгор метавонад раванди таълимро самаранок ва ҷолибтар созад.
Модели назарӣ бояд мантиқан ба фактҳои ҷойдошта мувофиқат кунад. Дар ҳақиқат, ҳар гуна илм ин модели назарии қисми муайяни олами воқеӣ ба ҳисоб меравад. Аксар вақт дар ҷараёни идрок объекти реалӣ О-ро бо дигар объекти идеалӣ, хаёлӣ ва ё материалии М, ки хусусиятҳои муҳимми объекти О-ро дар бар мегирад, иваз мекунанд ва онро модел ном мебаранд. Минбаъд бо модел таҷриба мегузаронанд, яъне, ба он бо ҳар гуна қувваҳо таъсир мерасонанд, параметрҳои онро тағйир медиҳанд ва чӣ тавр иваз шудани ҳолати онро ошкор месозанд. Дар мавриди мусбат анҷом ёфтани натиҷаи таҷриба бо объекти М онро ба объекти О интиқол медиҳанд. Ҳамин тариқ, модел-ин объекти материалӣ ва ё идеалӣ буда, тасвири содакардашудаи объекти реалӣ, ягон раванд ва ё ҳодиса ба шумор меравад.
Мақсадҳои асосии моделиронӣ инҳоанд:
► дарк намудани моҳияти объекти таҳқиқшаванда;
► омӯхтани идоракунии объект ва муайян сохтани тарзи беҳтарини идоракунӣ;
► пешгӯии оқибатҳои система дар шароити нав дар зери таъсири омилҳои беруна;
► ҳалли масъалаҳои амалӣ, оптимизатсияи фаъолияти системаи таҳқиқшаванда.
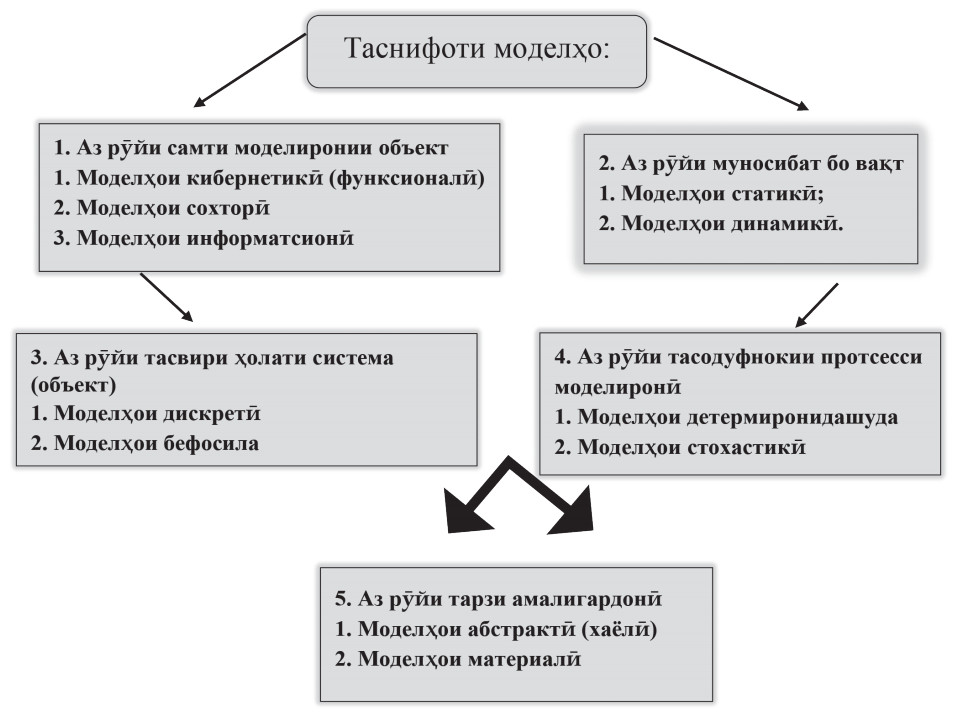
Намудҳои гуногуни моделҳо
Моделҳои мавҷудбуда бениҳоят гуногунранганд. Таҳлили системавӣ талаб менамояд, то онҳоро тасниф ва ба системаи муайян ворид кунем.

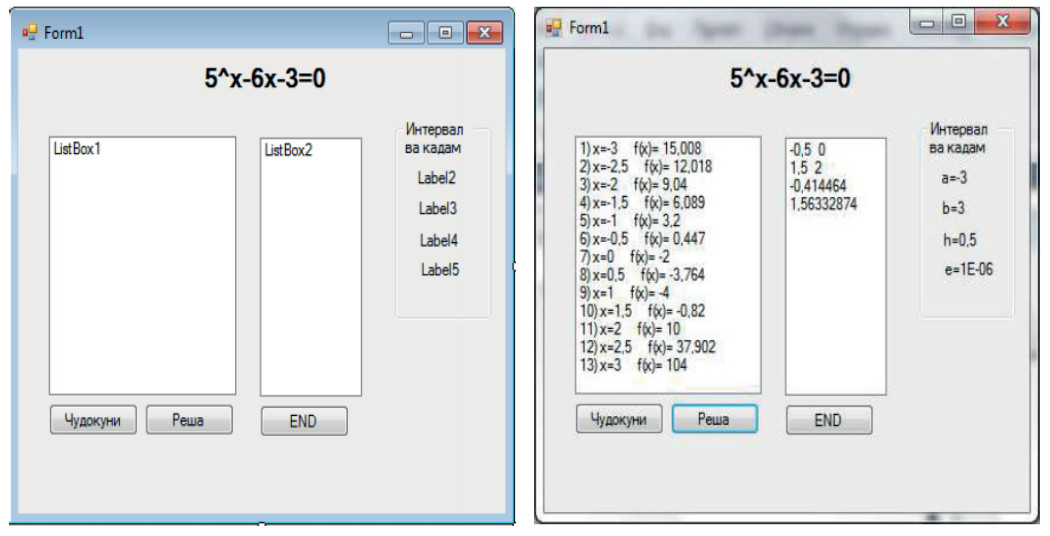
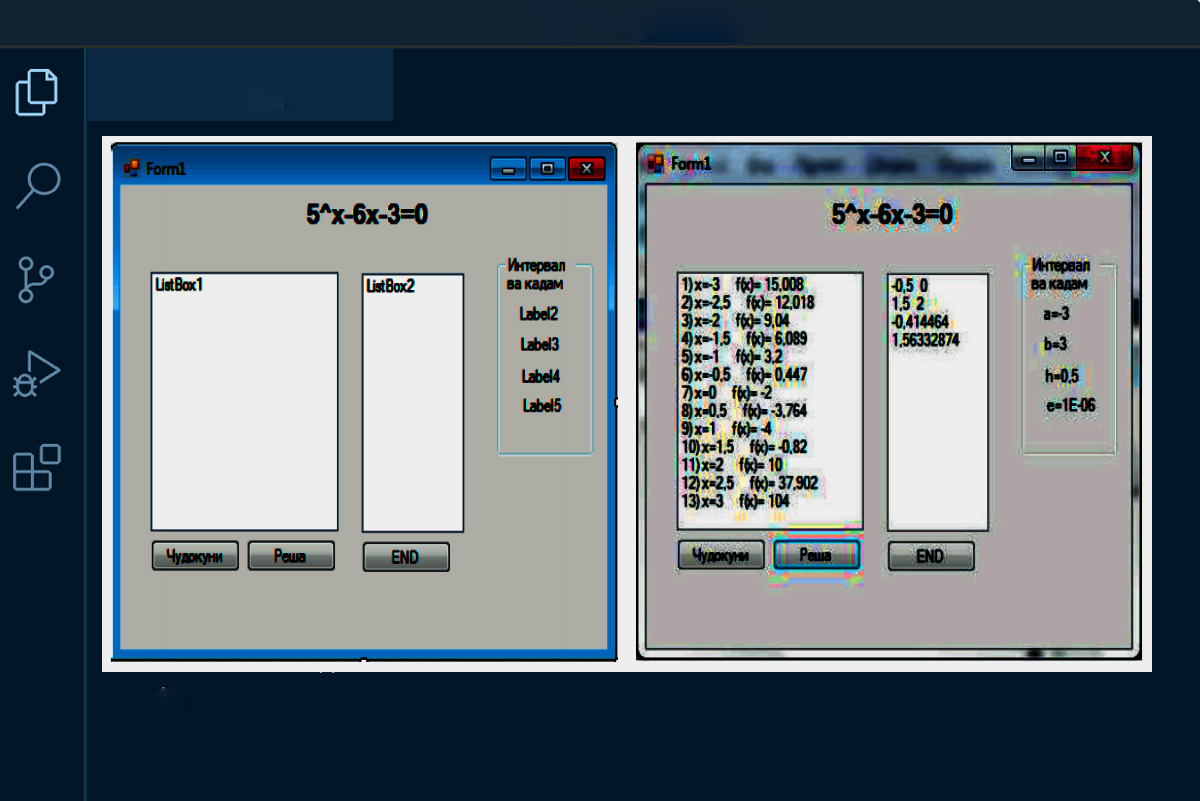
Намунаи 1. Моделиронии ададӣ.
Сохтани модели компютерии бо тарзи аналитикӣ ва графикӣ ҷудокунии решаи муодилаҳои алгебравӣ ва транстсендентӣ.
Дар амалия аксар вақт бо муодилаҳое дучор мешавем, ки онҳоро бо тарзи муқаррарӣ ҳал кардан ғайриимкон аст. Бинобар ин, усулҳои ёфтани ҳалли тақрибии муодилаҳо ва баҳодиҳии саҳеҳнокии онҳо мавқеи хосро ишғол мекунанд. Пеш аз он ки модели компютерии тарзи ҷудокунии решаи муодилаҳоро тартиб диҳем, моро лозим аст, ки сараввал модели математикии онро омӯзем.
Бигузор, муодилаи зерин дода шуда бошад f (x) = 0, (1), ки дар ин ҷо f (x) функсияи дар ягон интервали маҳдуд ва ё номаҳдуди a<x<b муайян ва бефосила аст. Ҳар гуна қимати x= с, ки дар он қимати функсия ба сифр баробар мегардад f (с) = 0, решаи муодилаи (1) ва ё нули функсияи f (x) номида мешавад. Барои ёфтани решаи ҳақиқии муодилаи (1) ду қадами зеринро иҷро намудан лозим аст:
1). Ҷудо намудани решаҳои муодила, яъне, чунин соҳаи хурди порча [a,b]-ро ёфтан лозим аст, ки дар он якто решаи муодила мавҷуд бошад.
2). Ёфтани реша бо саҳеҳии додашуда.
Барои иҷрои қадами якум ду тарзи ҷудокунии решаҳои муодилаҳо мавҷуд мебошад: аналитикӣ ва графикӣ. Теоремаи зеринро дида мебароем.
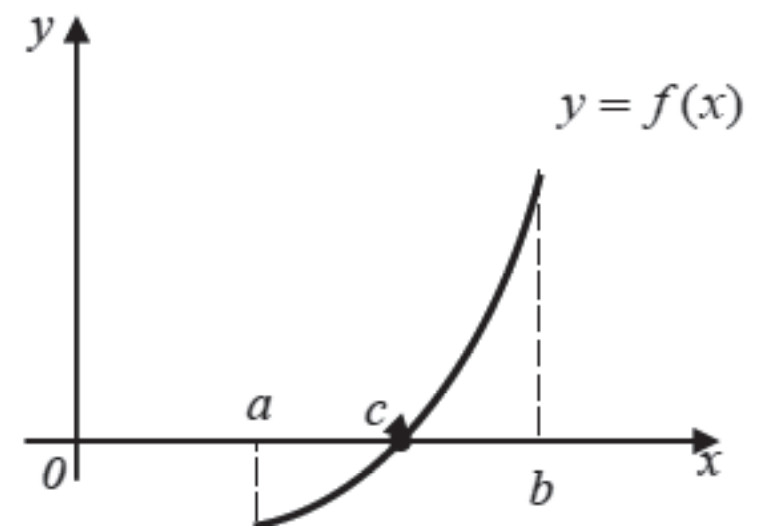
Теорема. Агар функсияи бефосилаи f (x) дар охирҳои порчаи [a,b] аломатҳои гуногунро қабул кунад, яъне, нобаробарии f (а).f (b) < 0 ҷой дошта бошад, он гоҳ дар дохили ин порча ақаллан якто ҳалли муодилаи f (x) = 0 мавҷуд аст. Илова бар ин, агар ҳосилаи тартиби якуми ин функсия дар дохили порча аломаташро иваз накунад, он гоҳ ин ҳал ягона мебошад.
Раванди ҷудокунии решаҳо аз муайян кардани аломати қимати функсияи f (x) дар нуқтаҳои сарҳадии x=a, x=b-и соҳаи мавҷудияти он оғоз мегардад. Сипас, аломати қимати функсияро дар як қатор нуқтаҳои мобайнии порча , ,… 1, 2 x = a ҳисоб мекунем, ки интихобе кадоме хос ба функсияи
f (x) мебошад.
Акнун раванди сохтани барномаи компютерии ҷудокунии реша ва то саҳеҳии додашуда аниқ ёфтани онро дида мебароем:

Imports System.Math
Public Class Form1
Dim f() As Single
Dim p(10) As Single, m As Byte
Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click
Dim i, n As Integer
Dim a, b As Integer, h, x As Single
a = InputBox(«a=») : Label2.Text = «a=» & a
b = InputBox(«b=») : Label3.Text = «b=» & b
h = InputBox(«h=») : Label4.Text = «h=» & h
n = (b — a) / h + 1
ReDim f(n)
i = 0 : ListBox1.Items.Clear()
For x = a To b Step h
i = i + 1
f(i) = Round(5 ^ x — 6 * x — 3, 3)
ListBox1.Items.Add(i & «) x=» & x & Space(5) & «f(x)= » & f(i))
Next x
For i = 1 To n — 1
If f(i) * f(i + 1) < 0 Then
m = m + 2
p(m — 1) = a + (i — 1) * h
p(m) = a + (i) * h
ListBox2.Items.Add(p(m — 1) & » » & p(m))
End If
Next
End Sub
Private Sub Button2_Click(sender As Object, e As EventArgs) Handles Button2.Click
End
End Sub
Function rewa(p1 As Single, p2 As Single) As Single
Dim e, c As Single
e = InputBox(«То сахехии е=») : Label5.Text = «e=» & e
Do
c = (p1 + p2) / 2
If (5 ^ p1 — 6 * p1 — 3) * (5 ^ c — 6 * c — 3) < 0 Then p2 = c Else p1 = c
Loop While p2 — p1 > e
rewa = c
End Function
Private Sub Button3_Click(sender As Object, e As EventArgs) Handles Button3.Click
ListBox2.Items.Add(rewa(p(1), p(2)))
ListBox2.Items.Add(rewa(p(3), p(4)))
End Sub
End Class